Posts

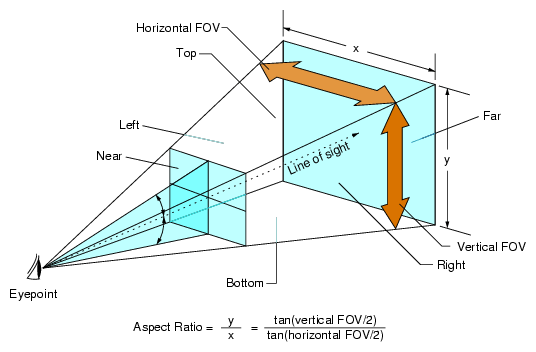
为什么要用GPU来进行蒙皮 对于一个SkinnedMeshRenderer，在做蒙皮的时候，对于每一个顶点，会先计算出这个顶点对应的四根骨骼的从骨骼空间到物体空间的矩阵\(M_{bone\localtoobject}\)，然后使用\(M{bone\localtoobject} * M{bone\bindpose} * Vertex{objectspace}\)得到经过骨骼平移旋转缩放后的四个带权重的顶点数据位置和切线，对于法线则是使用上面矩阵的逆矩阵的转置。然后对获得的位置、法线和切线，用权重计算得到经过骨骼平移旋转缩放后的实际的顶点信息。在通常的渲染过程中，上述操作是在CPU中进行的，最后把顶点数据传递给GPU中进行渲染。在顶点数较多且主要是矩阵运算的情况下，CPU进行蒙皮的效率就不如高并行的GPU了，因此会考虑到在GPU中进行蒙皮处理。 GPU蒙皮的一些想法 从上面可以看到，要从CPU中传给GPU的数据有以下几种：一是\(M_{bone\localtoobject} * M{bone\_bindpose}\)这样骨骼数个float4x4的矩阵，但是由于其最后一行是(0, 0, 0, 1)，在传递时可以简化成骨骼数个float3x4矩阵，这些矩阵每一帧都要传递一次；二是每个顶点对应的骨骼编号和骨骼的权重，骨骼编号用来查询骨骼矩阵中对应的矩阵，是一个整型的数据，骨骼权重是一个[0, 1]的小数，可以用\(BoneIndex + BoneWeight * 0.5\)的方式，把编号和权重结合成一个float的数据，这样每个顶点的骨骼编号和权重数据是一个float4的数据，可以保存在UV中，也可以用数组的方式传递给GPU，这些顶点数个float4的数据，只需要传递一次就可以了；再有就是模型本身的顶点位置、法线和切线，这些引擎会自动为我们传递给GPU。 在实际操作中，网上通常找到的方案是把动画保存在一张贴图或者是一个自定义的数据结构中，这里可以直接保存顶点数据，甚至不需要在GPU中做蒙皮的操作，但是随着顶点数增加会占用大量的空间；或者是保存骨骼的变换矩阵，在GPU中进行蒙皮，相对来说储存空间会小很多。然而我认为这两种都不是很好的做GPU skinning的方法，将动画信息保存到贴图或者数据结构中，会很大程度上失去Animator Controller的功能，如两个动作之间的插值、触发事件等，对于动画来说甚至是得不偿失的一种效果。因此，我希望能够保留Animator Controller的特性，实时的把骨骼数据传送给GPU，在GPU中进行蒙皮操作。 GPU蒙皮的操作 我的想法是，先离线从SkinnedMeshRenderer中获得骨骼的ID和权重，然后实时的从Animator Controller对应的骨骼中获取每根骨骼的骨骼矩阵，再统一传给一个普通的MeshRenderer，在GPU中进行蒙皮的操作。这中间有一个小坑，Unity同一个模型的SkinnedMeshRenderer和MeshRenderer，他们虽然都能获取到boneweight和bindpose，但是SkinnedMeshRenderer和MeshRnederer的骨骼的顺序有时候会有一些差异，因此最好的办法是，抛弃这两者的骨骼顺序，用Hierarchy中的骨骼顺序来确定我们传给GPU的boneindex，boneweight和bonematrix是一致的。 这里使用的模型及动作是mixamo的hip hop dancing资源。 BoneMatchInfo.cs 这个脚本的作用是，在离线时把一个GameObjectRoot下的所有SkinnedMeshRenderer和Hierarchy中的骨骼的信息结合起来，保存成一个Asset，用于实时的GPU Skinning。这个Asset包含两部分的信息，一个是BoneMatchNode用于记录Hierarchy骨骼列表中骨骼的名称和其bindpose，另一个是BindIndex用于记录所有SkinnedMeshRenderer的骨骼在Hierarchy骨骼列表中的顺序。 using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEditor; using System; using System.IO; namespace GPUSkinning { [System.Serializable] public class BoneMatchNode { //[HideInInspector] public string boneName; //在查找位于所有Transfom的位置时，设置并使用boneIndex public int boneIndex = 0; public Matrix4x4 bindPose; public BoneMatchNode(string _boneName) { boneName = _boneName; bindPose = Matrix4x4....

为什么要从深度图重建世界坐标 一个很大的应用情景是在后处理的阶段，或是计算一些屏幕空间的效果（如SSR、SSAO等），只能获取到一张深度贴图，而不是每一个几何体的顶点数据，很多的计算中却又需要用到世界坐标或者是视空间的坐标，这时我们就需要通过深度图来重建世界空间的坐标。 重建世界坐标的流程 首先要获取屏幕空间的UV，这里记为positionSS，范围是(0, 1)(0, 1)。 使用UV采样深度贴图，获取到当前的深度值。 使用UV和深度值，得到标准化设备坐标，这里记为positionNDC。 使用裁剪空间到视空间的变换矩阵乘以positionNDC，除以W分量，得到视空间坐标，这里记为positionVS。 使用视空间到世界空间的变换矩阵乘以positionVS，得到世界空间坐标，这里记为positionWS。 这里使用DepthToPositionShader.shader，假装是屏幕后处理的shader，来演示一下重建世界坐标的流程，这样比直接写屏幕后处理的shader能够更好的去了解Unity的空间变换的方式。 这个shader有以下几个需要注意的点： 为了使用_CameraDepthTexture这张深度贴图，需要在srp的设置中开启Depth Texture这个选项。这样子在渲染的时候会在DepthPrePass用shader中的Depth Only这个pass去先渲染出深度贴图。我们就能够在渲染物体的时候直接拿到包含当前物体的深度贴图了。 顶点着色器和片元着色器中的SV_POSITION并不完全相同。对于顶点着色器来说，SV_POSITION就是之前所说的\((\frac X {\tan {\frac {fovy} 2} \cdot \frac x y }, -\frac Y {\tan {\frac {fovy} 2}}, \frac {Zn} {f - n} + \frac {fn} {f - n}, -Z)\)；但是在片元着色器中，SV_POSITION的XY分量会乘上屏幕的宽高，Z分量则是已经除以W之后的深度值。屏幕的宽高信息保存在_ScreenParams这个内置的变量中，它的前两位是屏幕的宽高像素数，后两位是宽高的像素数的倒数加一。 要针对DX11和OpenGL不同的透视变换矩阵来调整UV的Y分量的数值，也就是要注意UNITY_UV_STARTS_AT_TOP这个宏的使用。出现获得的坐标跟随着摄像机的移动发生奇怪的倾斜的时候，往往都是忘记对Y分量的平台差异进行处理。 最后得到的视空间和世界空间的坐标值，要记得除以这个坐标值的W分量，相当于是做了一次归一化，才能得到正确的坐标。 DepthToPositionShader.shader Shader "zznewclear13/DepthToPositionShader" { Properties { [Toggle(REQUIRE_POSITION_VS)] _Require_Position_VS("Require Position VS", float) = 0 } HLSLINCLUDE #include "Packages/com.unity.render-pipelines.core/ShaderLibrary/Common.hlsl" #include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/core.hlsl" #pragma multi_compile _ REQUIRE_POSITION_VS sampler2D _CameraDepthTexture; struct Attributes { float4 positionOS : POSITION; float2 texcoord : TEXCOORD0; }; struct Varyings { float4 positionCS : SV_POSITION; float2 texcoord : TEXCOORD0; }; Varyings Vert(Attributes input) { Varyings output = (Varyings)0; VertexPositionInputs vertexPositionInputs = GetVertexPositionInputs(input....

空间变换和平台差异 将一个物体渲染到我们的屏幕上，需要经过一系列的坐标变换，这些坐标变换是在shader中使用矩阵进行计算的。变换的顺序如下，从物体空间(Object Space)到世界空间(World Space)，从世界空间到视空间(View pace)，从相机控件到裁剪空间(Clip Space)，最后显示到我们的屏幕空间(Screen Space)。 这一部分讲的空间变换是在Unity之外的空间变换，具体的Unity的空间变换还需要看这里。 物体空间到世界空间 这里用到的矩阵相对比较简单。我们用\(R\), \(T\)和\(S\)来分别代表物体的旋转平移和缩放系数，\(R\)由物体的三个旋转角决定，这里的格式是一个3x3的矩阵，\(T\)和\(S\)是两个1x3的向量，用\(P\)来代表物体空间的一个点。那么这个点在世界空间中的坐标就可以使用下面的式子进行计算： $$ P_{world} = \begin{pmatrix} R_{00} S_x& R_{01}& R_{02}& T_x \cr R_{10}& R_{11} S_y& R_{12}& T_y \cr R_{20}& R_{21}& R_{22} S_z& T_z \cr 0& 0& 0& 1 \end{pmatrix} \times \begin{pmatrix} P_x \cr P_y \cr P_z \cr 1 \end{pmatrix} $$ 这个4x4的矩阵就是物体空间到世界空间的变换矩阵，这里记为\(M_{o\to w}\)，在\(P\)的基础上额外增加了一个维度的这个向量，是\(P\)对应的齐次坐标。对于普通的向量\(V\)（如物体表面切线方向、视线方向、光源方向）等，从物体空间变换到世界空间时，齐次坐标的高次位应当为0，上式变为： $$ V_{world} = \begin{pmatrix} R_{00} S_x& R_{01}& R_{02}& T_x \cr R_{10}& R_{11} S_y& R_{12}& T_y \cr R_{20}& R_{21}& R_{22} S_z& T_z \cr 0& 0& 0& 1 \end{pmatrix} \times \begin{pmatrix} V_x \cr V_y \cr V_z \cr 0 \end{pmatrix} $$ 要注意的是：将物体空间的法线\(N\)变换到世界空间时，应当使用\(M_{o\to w}\)的逆矩阵的转置\((M_{o\to w}^{-1})^T\)，也就是世界空间到物体空间的变换矩阵的转置\((M_{w\to o})^T\)乘物体空间的法线\((M_{w\to o})^T \times N\)，这条式子等价于\(N \times M_{w\to o}\)。而对于正交矩阵来说，其逆矩阵就是这个矩阵的转置，因此可以像普通向量一样处理法线。...

什么是有向距离场以及它能用来干什么 有向距离场记录的是从一个点到集合边界的的距离值，其值的正负对应该点在集合外部或内部。有向距离场有很广的应用范围可以用来简单的生成Voronoi图形，可以用来做全局光照的计算，可以用来做两个形状的平滑的变形，可以用来做高清晰度的字体，也可以用来做Ray March（虽然我认为不如直接光线追踪求交来的效率高）。像原神就使用了SDF的方法，生成了角色脸部的阴影图，从而让角色脸部的阴影能自然的变化。 那么什么又是Jump Flooding Algorithm呢 Jump Flooding Algorithm是荣国栋在他的博士论文Jump Flooding Algorithm On Graphics Hardware And Its Applications提出的一种在GPU上运行的能够快速传播某个像素的信息到其他像素的算法。 普通的Flooding算法在一次运行中，固定向相邻的一个像素的像素传播信息，而Jump Flooding则是按照2的幂次递增或是递减来传播信息。这和之前提到的并行计算——Reduction的想法差不多。下图演示了普通的Flooding和Jump Flooding的过程： 使用JFA计算一张2D图片对应的SDF贴图 首先在Unity中创建JumpFlooding.cs, JFAComputeShader.compute, 和JFAVisualize.shader，分别用来执行Compute Shader，使用JFA算法计算SDF和可视化JFA算法的结果。 这里使用一张RGB通道为灰色，Alpha通道写着“JFA”的贴图作为我们2D图片的输入。 整体思路和需要注意的事项 先从简单实现功能上来考虑，暂时忽略掉抗锯齿的需求，直接对Alpha通道的值按照0.5来划分出图形的内部和外部，大于等于0.5为外部，小于0.5为内部。 SDF需要要计算距离，这里使用像素点中心到另一个像素点中心的距离（也可以使用像素点左下角到另一个像素点左下角的距离，不过为了明确起见，还是加上这半个像素的偏移比较好）。距离可以用uv的大小来表示，也可以用像素数量来表示，针对图像长宽不同的情况，这里以一个像素宽度为1来表示两个像素点的距离。在最后采样JFA的Render Texture的时候，也要注意使用sampler_PointClamp来进行采样，计算距离时也不能仅仅使用uv来计算，而是要使用像素中间的点的位置来进行计算。 普通的JFA算法会使用到Render Texture的两个通道，来标记像素对应的最近边界像素的UV，由于记录的是UV的数值而不是颜色信息，Render Texture要储存在线性空间中。由于要同时计算内部和外部的点到边界的有向距离，JFA算法会使用到Render Texture全部的四个通道，这里使用前两位记录位于内部的像素对应的边界像素的坐标，用后两位记录位于外部的像素对应的边界像素的坐标，即对于内部的像素(nearestUV.x, nearestUV.y, Z, W)，对于外部的像素(X, Y, nearestUV.x, nearestUV.y)，XYZW则可以用来表示该点为最初始的内外部的点、包含JFA传递的信息的点。不包含JFA传递的信息的点。 在JFA计算之前，需要先让贴图对应的点包含JFA信息，也就是说，对于内部的点初始化为(UV.x, UV.y, -1, -1)，对于外部的点初始化为(-1, -1, UV.x, UV.y)。这要求我们使用的Render Texture格式为至少R16G16B16A16 SFloat。 在JFA的计算中，以外部的像素点为例，所进行的操作是：采样上次经过JFA操作的Render Texture；根据XY通道判断该点在边界的内部还是外部，内部就跳过；对外部的像素点，通过XY通道判断是否已包含JFA的信息，如果包含，根据ZW通道计算出当前点到其包含的最近像素的距离，如果不包含，将这个距离设置为一个极大的常数；分别采样距离像素点2的幂次的距离的八个像素，判断这些像素是否已包含JFA的信息，如果不包含，采样下一个点，如果包含，根据这些像素的ZW通道计算出当前点到这些像素包含的最近像素的距离，并和上一步算出的距离进行比较，如果小于上一步算出的距离，则证明该像素对应的最近像素为周围点包含的像素，更新该像素的ZW通道，并且将XY通道标记成已包含JFA的信息。 采样周边像素的步长从2D贴图的长宽的一半向上取整开始，每次JFA都取上一步步长的一半向上取整作为新的步长，一直进行到步长为(1, 1)，进行最后一次JFA计算。 经过JFA计算之后，还需要将分别表示内部的点对应的最近像素的UV和外部的点对应的最近像素的UV结合起来，储存为一张贴图，可以是(nearestUV.x, nearestUV.y, 0, inside?1:0)，也可以是(distance * inside?-1:1, 1)。 应该是跟当前平台有关，有时候会出现贴图上下颠倒的情况，可以用UNITY_UV_STARTS_AT_TOP来协助解决，不过compute shader可能需要自己启用这个宏，这里就直接硬写在shader里，不做平台判断了。 JFAComputeShader.compute 根据上面的整体思路，我们需要三个kernel，一个用来初始化，一个做JFA计算，最后一个用来合成最后的贴图。Compute Shader的关键字需要Unity 2020以上（我也不知道具体哪个版本）才能有，这里就暂时用UNITY_2020_2_OR_NEWER这个宏来屏蔽了。 #pragma kernel CopyUVMain #define PIXEL_OFFSET 0....

为什么要用球谐函数来计算全局光照 在物体的渲染中，除了计算直接光照的BRDF之外，也要计算间接光照对物体的影响。在引擎中获取间接光照信息的方法通常是在场景中布置一个反射探针，离线渲染一个360度的场景贴图。这样在计算间接光照的高光部分的时候，可以使用视线在物体上的反射方向reflect(-viewDirection, normal)，对渲染好的贴图进行采样，再进行brdf的计算，因此这张贴图也会被称作是specular map；然而在计算间接光照的漫反射部分时，因为目标点会受到来自各个方向上的光线带来的漫反射，不能再简单的使用视线的反射来采样这张帖图。这时有两种解决办法，一种是采样这张贴图的mipmap，在一定程度上模糊的mipmap可以认为是综合了各个方向的光照的信息，另一种则是Ravi Ramamoorthi和Pat Hanrahan2001年在An Efficient Representation for Irradiance Environment Maps中提出的，通过球谐函数重新构建低频光照信息的方式，将其作为简介光漫反射部分的贴图。 如何使用球谐函数重新构建光照信息 在Ravi Ramamoorthi的论文中他给出了球谐参数的计算公式和重构光照信息的公式： $$ \tag*{球谐参数} L_{lm} = \int_{\theta = 0}^\pi\int_{\theta = 0}^{2\pi}L(\theta)Y_{lm}(\theta, \phi)sin\theta d\theta d\phi $$ $$ \begin{align*}其中(x, y, z) &= (sin\theta cos\phi, sin\theta sin\phi, cos\theta) \cr Y_{00}(\theta, \phi) &= 0.282095 \cr (Y_{11};Y_{10};Y_{1-1})(\theta, \phi) &= 0.488603(x;z;y) \cr (Y_{21};Y_{2-1};Y_{2-2})(\theta, \phi) &= 1.092548(xz;yz;xy) \cr Y_{20}(\theta, \phi) &= 0.315392(3z^2 - 1) \cr Y_{22}(\theta, \phi) &= 0.546274(x^2 - y^2) \end{align*} $$ $$ \tag*{重构光照} \begin{equation}\begin{split} E(n) =&\ c_1L_{22}(x^2 - y^2) + c_3L_{20}z^2 + c_4L_{00} - c_5L_{20} \cr +&\ 2c_1(L_{2-2}xy + L_{21}xz + L_{2-1}yz) \cr +&\ 2c_2(L_{11}x + L_{1-1}y + L_{10}z)\end{split}\end{equation} $$ $$ 其中c1 = 0....