空间变换和平台差异
将一个物体渲染到我们的屏幕上,需要经过一系列的坐标变换,这些坐标变换是在shader中使用矩阵进行计算的。变换的顺序如下,从物体空间(Object Space)到世界空间(World Space),从世界空间到视空间(View pace),从相机控件到裁剪空间(Clip Space),最后显示到我们的屏幕空间(Screen Space)。
这一部分讲的空间变换是在Unity之外的空间变换,具体的Unity的空间变换还需要看这里。
物体空间到世界空间
这里用到的矩阵相对比较简单。我们用\(R\), \(T\)和\(S\)来分别代表物体的旋转平移和缩放系数,\(R\)由物体的三个旋转角决定,这里的格式是一个3x3的矩阵,\(T\)和\(S\)是两个1x3的向量,用\(P\)来代表物体空间的一个点。那么这个点在世界空间中的坐标就可以使用下面的式子进行计算: $$ P_{world} = \begin{pmatrix} R_{00} S_x& R_{01}& R_{02}& T_x \cr R_{10}& R_{11} S_y& R_{12}& T_y \cr R_{20}& R_{21}& R_{22} S_z& T_z \cr 0& 0& 0& 1 \end{pmatrix} \times \begin{pmatrix} P_x \cr P_y \cr P_z \cr 1 \end{pmatrix} $$ 这个4x4的矩阵就是物体空间到世界空间的变换矩阵,这里记为\(M_{o\to w}\),在\(P\)的基础上额外增加了一个维度的这个向量,是\(P\)对应的齐次坐标。对于普通的向量\(V\)(如物体表面切线方向、视线方向、光源方向)等,从物体空间变换到世界空间时,齐次坐标的高次位应当为0,上式变为: $$ V_{world} = \begin{pmatrix} R_{00} S_x& R_{01}& R_{02}& T_x \cr R_{10}& R_{11} S_y& R_{12}& T_y \cr R_{20}& R_{21}& R_{22} S_z& T_z \cr 0& 0& 0& 1 \end{pmatrix} \times \begin{pmatrix} V_x \cr V_y \cr V_z \cr 0 \end{pmatrix} $$ 要注意的是:将物体空间的法线\(N\)变换到世界空间时,应当使用\(M_{o\to w}\)的逆矩阵的转置\((M_{o\to w}^{-1})^T\),也就是世界空间到物体空间的变换矩阵的转置\((M_{w\to o})^T\)乘物体空间的法线\((M_{w\to o})^T \times N\),这条式子等价于\(N \times M_{w\to o}\)。而对于正交矩阵来说,其逆矩阵就是这个矩阵的转置,因此可以像普通向量一样处理法线。
世界空间到视空间
和上面的物体空间到世界空间基本一致,但是从这里开始坐标系的手性会对变换使用的矩阵产生巨大的影响,可以说是一切混乱的开端。在OpenGL这样的右手系图形API中,摄像机往往看向Z轴的负方向,因此物体的视空间坐标的Z分量是负值;而对于左手系的坐标系,如DirectX的注明左手系的函数(D3DXMatrixLookAtLH),摄像机看向Z轴的正方向,物体的视空间坐标的Z分量是正值。
视空间到裁剪空间
从这里开始就不再是像之前那样简单的坐标变换了,这里以最常用到的透视变换为例。
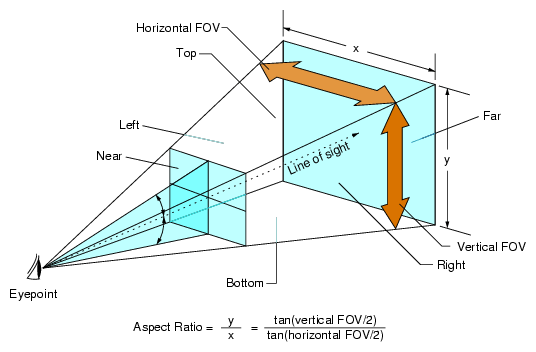
摄像机的参数如fov、远近裁剪面在这个坐标变换的过程中影响了最终的结果,我们这里用\(fovy\)表示摄像机竖直方向上张开的角度,用\(\frac y x\)表示摄像机图像的高宽比(AspectRatio,在DirectX中往往用的是\(\frac x y\)),用\(near\)和\(far\)表示摄像机的远近裁剪面。这里给出一张OpenGL的摄像机裁剪空间示意图,来自OpenGL Performer™ Getting Started Guide:

对于OpenGL,使用的透视变换矩阵如下:
$$ \begin{pmatrix} \frac 1 {\tan {\frac {fovy} 2} \cdot \frac x y }& 0& 0& 0 \cr 0& \frac 1 {\tan {\frac {fovy} 2}}& 0& 0 \cr 0& 0& - \frac {f + n} {f - n}& - \frac {2fn} {f - n} \cr 0& 0& -1& 0 \end{pmatrix} $$
对于视空间点\(P = (X, Y, Z, 1)\)(这里的Z往往是负值),这个矩阵将其变换到
$$ P_{clip space} = (\frac X {\tan {\frac {fovy} 2} \cdot \frac x y }, \frac Y {\tan {\frac {fovy} 2}}, -\frac {Z(f + n)} {f - n} - \frac {2fn} {f - n}, -Z) $$
将这个新的坐标的XYZ分量除以W分量,就能把XYZ坐标在(-X, X)(-Y, Y)(-N, -F)范围的点映射到(-1, 1)(-1, 1)(-1, 1)了。
对于左手系的坐标系,如DirectX中注明左手系的D3DXMatrixPerspectiveFovLH,使用的透视变换矩阵如下,这里相当于对DirectX的CPU中的矩阵进行了转置(和Shader中的矩阵一致),这样更好理解:
$$ \begin{pmatrix} \frac 1 {\tan {\frac {fovy} 2} \cdot \frac x y }& 0& 0& 0 \cr 0& \frac 1 {\tan {\frac {fovy} 2}}& 0& 0 \cr 0& 0& \frac f {f - n}& -\frac {fn} {f - n} \cr 0& 0& 1& 0 \end{pmatrix} $$ 对于视空间点\(P = (X, Y, Z, 1)\)(这里的Z往往是正值),这个矩阵将其变换到 $$ P_{clip space} = (\frac X {\tan {\frac {fovy} 2} \cdot \frac x y }, \frac Y {\tan {\frac {fovy} 2}}, \frac {Zf} {f - n} - \frac {fn} {f - n}, Z) $$
将这个新的坐标的XYZ分量除以W分量,就能把XYZ坐标在(-X, X)(-Y, Y)(N, F)范围的点映射到(-1, 1)(-1, 1)(0, 1)了。
这里可以看到左手系DirectX和OpenGL的区别:首先是视空间坐标Z分量的区别,DirectX是正值,而OpenGL是负值;其次是计算得到的深度值的区别,DirectX近裁剪面是0,远裁剪面是1,OpenGL近裁剪面是-1,远裁剪面是1。同时因为浮点数精度在0的时候比较高,为了让线性的深度能够尽可能平均的分布到浮点数中,会有Reverse Z的考虑,即会使远裁剪面为0,近裁剪面为1,对于DirectX,只需要交换near和far的数值就可以了。
裁剪空间到屏幕空间
虽然经过上一步变换的坐标的,除以W分量后的XYZ分量乘2减1(DirectX的Z分量不需要乘2减1),已经是我们想要的标准化设备坐标(Normalized Device Coordinate, NDC)了:
//DX11
float3 Pndc = float3((Pclip.xy / Pclip.w) * 0.5 + 0.5, Pclip.z / Pclip.w);
//OpenGL
float3 Pndc = (Pclip.xyz / Pclip.w) * 0.5 + 0.5;
由于裁剪空间并不是线性变化的,考虑到从顶点着色器到片元着色器时的线性插值会受到透视变形的影响,Unity中的NDC只做了乘2减1这一步,而没有除以W分量。
相关的代码可以在ShaderVariablesFunctions.hlsl中看到:
VertexPositionInputs GetVertexPositionInputs(float3 positionOS)
{
VertexPositionInputs input;
input.positionWS = TransformObjectToWorld(positionOS);
input.positionVS = TransformWorldToView(input.positionWS);
input.positionCS = TransformWorldToHClip(input.positionWS);
float4 ndc = input.positionCS * 0.5f;
input.positionNDC.xy = float2(ndc.x, ndc.y * _ProjectionParams.x) + ndc.w;
input.positionNDC.zw = input.positionCS.zw;
return input;
}
_ProjectionParams.x用于处理DX11和OpenGL的Y分量相反的情况,类似于UNITY_UV_STARTS_AT_TOP。先乘0.5再加W分量,等价于上面的计算NDC的式子不除以W分量。
切线空间到世界空间
在使用法线贴图的时候,也经常会用到切线空间和世界空间的转换。和之前的转换不同的是,我们并不能从预先设定好的宏中获取切线空间到世界空间的变换矩阵,而是知道世界空间的切线Tangent、双切线Bitangent和法线Normal的值,这里记为\(T, B, N\)。我们可以利用这三个世界空间 的向量来计算切线空间中向量\(V\)的世界空间表示: $$ V_{world} = \begin{pmatrix} T_x& B_x& N_x \cr T_y& B_y& N_y \cr T_z& B_z& N_z \end{pmatrix} \times \begin{pmatrix} V_x \cr V_y \cr V_z \end{pmatrix} $$
这里也稍微解释一下为什么Unity在计算双切线的时候要乘上切线的w分量。一般情况下切线是uv的x轴正方向,双切线是uv的y轴正方向。由于部分建模软件的手性与Unity不一致,Unity中使用法线叉乘切线计算得到的双切线与建模软件生产出的模型的uv的y轴正方向就会相反,这样在采样建模软件生产的法线贴图的时候,由于两者相反,计算出来的凹凸效果看上去就会是反着的。为了解决这个问题,Unity在模型导入检测到手性不一致的时候,会将切线的w分量设置成-1,这样在做切线空间的变换的时候,模型的uv能正确对应切线和双切线,从而可以得到正确的变换后的法线。
Unity中的空间变换
为此Unity定义了一系列的宏用来记录这些变换中对应的矩阵:UNITY_MATRIX_M, UNITY_MATRIX_V, UNITY_MATRIX_P以及这些矩阵的逆矩阵和这些矩阵相乘所得的矩阵,这些宏的定义可以在Input.hlsl中找到。
同时Unity也定义了一系列的方便进行坐标转换的函数,可以在SpaceTransforms.hlsl中找到。
全平台和Unity历史遗留的矛盾
Unity最一开始是MacOS上的游戏引擎,因此Unity最初是使用OpenGL的,这也就导致了一开始Unity就使用的是右手系的坐标系。随着逐渐的发展,Unity也使用了DirectX之类的左手系的图形API,甚至Unity的世界空间就是一个左手系的坐标系。但是出于某些原因(积重难返),Unity的视空间矩阵UNITY_MATRIX_V使用的是OpenGL的右手系矩阵(相机看向Z轴负方向)。也就是说使用UNITY_MATRIX_V计算得到的视空间的坐标,其Z分量往往是小于0的。而unity_WorldToCamera才是正常应当使用的相机的变换矩阵(相机看向Z轴正方向的左手系矩阵)。这也就导致了UNITY_MATRIX_P和上面所说的矩阵也略有不同,除了Reverse Z的操作之外,在DX11的API下,Unity翻转了UV的Y分量,并且把投影矩阵第四行第三列的1改成了-1。
详情可以看bgolus的解释。
这里也放一下Unity中的别扭的DX11的矩阵:
$$ M_{\text{UNITY\_MATRIX\_P}} = \begin{pmatrix} \frac 1 {\tan {\frac {fovy} 2} \cdot \frac x y }& 0& 0& 0 \cr 0& -\frac 1 {\tan {\frac {fovy} 2}}& 0& 0 \cr 0& 0& \frac n {f - n}& \frac {fn} {f - n} \cr 0& 0& -1& 0 \end{pmatrix} $$
对于视空间点\(P = (X, Y, Z, 1)\)(这里的Z往往是负值),这个矩阵将其变换到
$$ P_{clip space} = (\frac X {\tan {\frac {fovy} 2} \cdot \frac x y }, -\frac Y {\tan {\frac {fovy} 2}}, \frac {Zn} {f - n} + \frac {fn} {f - n}, -Z) $$
将这个新的坐标的XYZ分量除以W分量,就能把XYZ坐标在(-X, X)(-Y, Y)(-N, -F)范围的点映射到(-1, 1)(1, -1)(1, 0)了。也就是说这个矩阵翻转了UV的Y分量,并且使用了Reverse Z来保证深度的精度。
行矩阵和列矩阵
在GPU运算中,HLSL使用的是行矩阵(与之相反,GLSL使用的是列矩阵)。在Shader中输入float4x4 M_temp = float4x4(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p),得到的矩阵是这样的:
$$ M_{temp} = \begin{pmatrix} a& b& c& d \cr e& f& g& h \cr i& j& k& l \cr m& n& o& p \end{pmatrix} $$
如果输入的是float4x4 M_temp = float4x4(row0, row1, row2, row3),得到的矩阵是这样的:
$$ M_{temp} = \begin{pmatrix} {row0}_x& {row0}_y& {row0}_z& {row0}_w \cr {row1}_x& {row1}_y& {row1}_z& {row1}_w \cr {row2}_x& {row2}_y& {row2}_z& {row2}_w \cr {row3}_x& {row3}_y& {row3}_z& {row3}_w \end{pmatrix} $$
因此,我们常常说的TBN矩阵,输入的是float3x3 TBN = float3x3(tangent, bitangent, normal),其对应的矩阵是:
$$ M_{TBN} = \begin{pmatrix} {tangent}_x& {tangent}_y& {tangent}_z \cr {bitangent}_x& {bitangent}_y& {bitangent}_z \cr {normal}_x& {normal}_y& {normal}_z \end{pmatrix} $$
这实际上是切线空间到世界空间的矩阵的转置,因此在计算的时候使用向量左乘这个矩阵mul(dirTS, TBN)能够将切线空间的向量转换到世界空间。
顺带一提,HLSL中矩阵的成员变量是这样排列的:
$$ M_{temp} = \begin{pmatrix} \_m00& \_m01& \_m02& \_m03 \cr \_m10& \_m11& \_m12& \_m13 \cr \_m20& \_m21& \_m22& \_m23 \cr \_m30& \_m31& \_m32& \_m33 \end{pmatrix} $$
这边有一小段Shadertoy代码,可以用来快速判断当前是行矩阵还是列矩阵,复制到Unity中也能用,亮色为当前矩阵与选定的矩阵类型相同:
GLSL Column Major
2024年3月15日修订
2022年修订的时候可想不到两年后我还得回来改这篇文章。当时写的时候一定是GLSL写太多了,而且并没有真正地用代码去检验是行矩阵还是列矩阵,以至于最近在重新做视差映射时,用列矩阵去看之前写的代码的时候,怎么想都觉得不对劲。实在是汗流浃背了。
2022年1月25日修订
只能说反转再反转吧,最一开始我就认为Unity的相机是看向Z轴负方向的(因为当时UNITY_MATRIX_V用的比较多),直到昨天在编辑器的窗口里看了一眼,发现在窗口里相机是看向Z轴正方向的(那么大一个蓝色的箭头),然后就开始了深深的自我怀疑。
直到询问了bgolus之后才真正的确定,Unity的视空间的变换矩阵UNITY_MATRIX_V是一个右手系的矩阵,其相机看向Z轴的负方向。只能说Unity确实有些别扭了。。。